Recherche / Research

Mise en forme / Shape morphing

Instabilités élastiques / Elastic instabilities
 

Fissures, friction délaminage / Cracks, friction, delamination

Élasto-capillarité / Elasto-capillarity

Interfaces & Instabilités / Interfaces & Instabilities
 

Mise en forme / Shape morphing

Curvy cuts: Programming axisymmetric kirigami shapes
with Marie Tani, Joo-Won Hong, Takako Tomizawa, Étienne Lepoivre & Benoît Roman

Although bending a sheet of paper is an easy operation, stretching is more limited and it leads to rupture and tears. However, well-designed cuts on the sheet can induce a large effective stretchability. We are here interested in the axisymmetric configuration where cuts are designed along concentric circles. Applying an increasing transverse load at the center of the sheet results into a 3D axisymmetric structure of growing amplitude which eventually saturates. Reversing the problem, we propose, a design procedure for the cuts leading to a desired 3D shape.
Extreme Mechanics Letters 71, 102195 (2024)

Pneumatic cells toward absolute Gaussian morphing
with Tian Gao & Benoît Roman

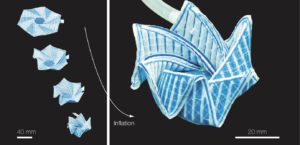On a flat map of the Earth, continents are inevitably distorted. Reciprocally, curving a plate simultaneously in two directions requires a modification of in-plane distances. Although emerging architectured materials with programmed in-plane distortions are capable of such shape morphing, an additional control of local bending is required to precisely set the final shape of the resulting three-dimensional surface. Inspired by bulliform cells in leaves of monocotyledon plants, we show how the internal structure of flat panels can be designed to program bending and in-plane distortions simultaneously when pressurized, leading to a targeted shell shape.
Science 381, 862 (2023)
Movies illustrating the deployment of the structures

Programming stiff inflatable shells from planar patterned fabrics
with Emmanuel Siéfert, Étienne Reyssat & Benoît Roman

We introduce a versatile single-step method to shape-program stiff inflated structures, opening the door for numerous large scale applications, ranging from space deployable structures to emergency shelters. This technique relies on channel patterns obtained by heat-sealing superimposed flat quasi-inextensible fabric sheets. Inflating channels induces an anisotropic in-plane contraction and thus a possible change of Gaussian curvature. Seam lines, which act as a director field for the in-plane deformation, encode the shape of the deployed structure. We present three patterning methods to quantitatively and analytically program shells with non-Euclidean metrics.
Soft Matter 16, 7898 (2020)
Movies illustrating the deployment of the structures

Programing curvilinear paths of flat inflatables
with Emmanuel Siéfert, Étienne Reyssat & Benoît Roman

Inflatable structures are flat and foldable when empty and both lightweight and stiff when pressurized and deployed. They are easy to manufacture by fusing 2 inextensible sheets together along a defined pattern of lines. However, the prediction of their deployed shape remains a mathematical challenge, which results from the coupling of geometrical constraints and the strongly nonlinear and asymmetric mechanical properties of their composing material: thin sheets are very stiff on extensional loads, while they easily shrink by buckling or wrinkling when compressed. We discuss the outline shape, local cross-section, and state of stress of any curvilinear open path. We provide a reverse model to design any desired curved 2-dimensional shape from initially flat tubes.
Proceedings of the National Academy of Sciences 116, 16692 (2019)
Journal of the Mechanics and Physics of Solids, 143, 104068 (2020)
Movie of a deployable « hello »

Baromorphs: pneumatic shape morphing elastomers
with Emmanuel Siéfert, Étienne Reyssat & Benoît Roman

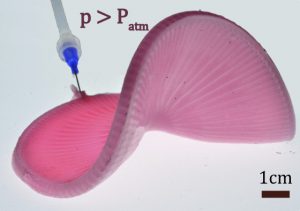Although bending a sheet of paper into a cylinder or a conical hat is quite easy, bending the same sheet in two simultaneous directions is not possible without crumples. However Nature is full of structures that are initially planar, but adopt complex 3D shapes as they grow. The secret of lettuce leaves? Differential growth: some regions, or some directions grow faster than the others.
Non-homogeneous growth with electroactive sheets could be a solution (see below). With the baromorphs, we chose the second strategy: non-isotropic growth. A network of channels is embedded inside an elastomer plate. Upon pressure, the channel tend to expend. This expansion is much higher across their section than along their length. Such growth is not compatible anymore with a planar geometry and the structure adopts a 3D shape that can be tuned by the pressure. In this example of material intelligence, the information is encoded the design of the channels.
What kind of shapes can be obtained with such technique? The simplest examples are domes or saddles obtained with circular of radial channels, respectively. In theory any reasonably smooth 3D shape can nevertheless be obtained by combining these two elementary geometries.
What applications do we envision? Soft robotics, and more specifically, equipments for disabled persons, adaptable furniture, but also deployable structures for space applications.
Nature Materials (2019)
News & Views from Efi Efrati
in ESPCI News, by Kevin Lamothe
in Wissenschaft aktuell by Jan Oliver Löfken
in Pour la Science by François Savatier

Instabilités élastiques / Elastic instabilities

Stretch induced bending
with Emmmanuel Siéfert, Nicolas Cattaud, Étienne Reyssat & Benoît Roman

Buckling of electroactive sheets
with Hadrien Bense, Miguel Trejo, Étienne Reyssat & Benoît Roman

We develop deformable dielectric membranes by depositing carbon black powder on the opposite faces of films of silicone rubber. When an electric field is applied, the membranes get compressed across their thickness, which results into an extension of the surface. If this effective growth is frustrated by the boundary conditions, the membrane buckles out of plane. We study the different 3D patterns obtained through this electro-mechanical instability.
Soft matter 13, 2876 (2017)

Compressed sheets
with Jérémy Hure & Benoît Roman

Sandwiching a plate into a spherical mold results into orthoradial wrinkles due to the mismatch in Gaussian curvatures between a sphere (positive curvature) and a plane (zero curvature).
The central region of the plate can accommodate this mismatch, and wrinkles only appear beyond the mid radius of the plate and progressively split in more wrinkles in the direction of the edges. The final wavelength decreases with the gap separating the parts fo the mold, but reaches a finite value when this gap is of the order of the thickness of the plate. Surprisingly the force required for compressing the wrinkled plate presents a maximum independent of the thickness.
Physical Review Letters 109, 054302 (2012)

Wrinkled curtains
with Hugues Vandeparre, Miguel Piñeirua, Fabian Brau, Benoît Roman, Cyprien Gay, W. Bao, Pedro Reis & Pascal Damman

Have you ever payed attention to the wrinkles formed in a suspended
curtain? The stitches usually induce relatively regular wrinkles (right picture). The number of wrinkles decreases progressively along the curtain.
Similar wrinkles are also observed at the minute scale of graphene films suspended over a grove (left image).
The evolution of the number of wrinkles follows intuition. Indeed a wrinkles propagating through the whole length of the curtain would generate a high elastic bending energy. Merging wrinkles progressively decreases this energy but nevertheless requires some stretching of the curtain.
Physical Review Letters 106, 224301 (2011)

Scars
with Atsushi Takei, Fabian Brau & Benoît Roman

Stretching an elastic sheet between a pair of opposite clamps induces a contraction through Poisson effect. While the stretching remains low out-of-plane deformations are not observed. Wrinkles however appear if the sheet is reinforced. Such morphology is also observed along scars on the skin.
In the case of the reinforcement by a fiber, we observe a transition to in-plane deformation of the fiber.
Europhysics Letters 96, 64001 (2011)

Fissures, friction délaminage / Cracks, friction, delamination

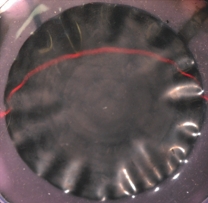
Self-replicating cracks
with Joël Marthelot, Jérémie Tesseire, Davy Dalmas, Étienne Barthel & Benoît Roman

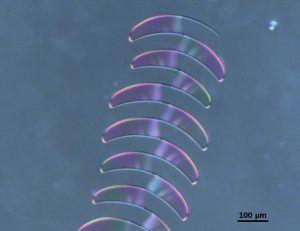
Thin films are ubiquitous in engineering applications ranging from protective paints for our homes to the optical layers deposited on our glasses. However, coating processes generally result into residual strains and may induce the propagation straight cracks, eventually leading to the familiar patterns seen on dried mud or crockery glaze.
We find that cracks can propagate in films considered as stable using standard engineering criteria, and form extremely regular patterns. Indeed, they follow intriguing paths such as Archimedean spirals, oscillating alleys or parallel stripes. A new fracture mechanism based on a coupling between delamination and crack propagation leads to the self-replication of an initial pattern. This mechanism selects a regular length scale of about 30 times the thickness, but independent from material properties.
Physical Review Letters 113, 085502 (2014)
Journal of the Mechanics and Physics of Solids 84, 214 (2015)

Guided tearing: the ruler test
with Alejandro Ibarra, Juan-Francisco Fuentealba,  Benoît Roman & Francisco Melo

Cracks in anisotropic sheets
with Atsushi Takei, Benoît Roman, Eugenio Hamm & Francisco Melo

Fracture is an old problem, yet a simple and fundamental question is still debated: in which direction does a crack propagate?
Although they are ubiquitous, the criterion for the selection of propagation direction still remains an open question. We propose a description for this selection based on a geometrical tool (Wulf plot) developed to predict the shape of crystals. As in crystals, forbidden directions may be found depending on the landscape of the fracture energy. This approach is confirmed with « trouser-test » experiments on thin sheets. Counter-intuitively, a crack may not always select the easiest direction of propagation but follow a local optimum.
A simple experiment of a packaging film for cookies can illustrate these features. Trying to force a crack to follow a forbidden direction with a ruler leads to a zigzagging instability! (left image: forbidden direction; right image: standard direction).
Physical Review Letters 110, 144301 (2013)

Friction and adhesion
with Suomi Ponce & Benoît Roman

We study the resistance upon traction of an elastomer strip adhering on a glass plate through van der Waals interactions. In the limit of vanishing peeling angles, we observe the propagation of a sliding front along the strip. The propagation of this front leads to a progressive increase of the traction force. The band suddenly detaches when the front reaches the end of the strip. We propose a mechanism based on a constant friction stress acting on the sliding region of the strip. This stress is on the order of 50 kPa, which is compatible with other studies dedicated to friction of polymers. This result is not singular. Indeed the effect of friction becomes more dominant as lower peeling angles are considered.
Soft matter 11, 9281 (2015)

Delamination blisters
with Dominic Vella, Pedro Reis, Arezki Boudaoud, Yuko Aoyanagi & Benoît Roman

Proceedings of the National Academy of Sciences 106, 10901 (2009)
Soft Matter 6, 5720 (2010)

Élasto-capillarité / Elasto-capillarity
Annual Review of Fluid Mechanics 50, 629 (2018)
MRS Bulletin 41, 108 (2016)
Journal of Physics: Condensed Matter 22, 493101 (2010)

Wet hair
with Benoit Roman , Charlotte Py , Arezki Boudaoud & Sébastien Neukirch

The hair of a dog coming out of a pond assemble into clumps giving him a spiny appearance. What is the number of hairs in a clump? The answer relies on a balance between capillary forces and elasticity of the hairs. More generally, the sticking of flexible elements dramatically damages mechanical microsystems or lung airways, but also allows beetles to climb on walls.
Nature 432, 690 (2004)
Europhysics Letters 77, 44005 (2007)
Journal of the Mechanics and Physics of Solids 55, 1212 (2007)
Physical Review E 76, 060102 (2007)
Europhysics Letters 90, 44006 (2010)

Capillary twist
with A. Legrain, E.J.W. Berenschot, L. Abelmann, J. Bico & N.R. Tas

We show the self-assembly through twisting and bending of side by side ribbons under the action of capillary forces. Micro-ribbons made of silicon nitride are batch assembled at the wafer scale. Model experiments are carried out at the macroscopic scale where the tension in ribbons can easily be tuned. The process is modeled considering the competition between capillary, elastic and tension forces. This simple self-assembly technique yields highly symmetric and controllable structures which could be used for batch fabrication of functional 3D micro-structures.
Soft matter 12, 7186 (2016)

Elastocapillary imbibition
with Thomas Cambau & Étienne Reyssat

We investigate the dynamics of the capillary rise of a liquid in a cell formed by parallel plates, one of which is flexible. Above a critical width, the cell collapses under the negative capillary pressure in the liquid. This collapse allows the liquid to rise virtually without limit between the plates. The height of the rising front is found to increase with time as t^1/3, a characteristic of capillary imbibition in a wedge.
Europhysics Letters 96, 24001 (2011)

Capillary Origami

with Benoit Roman , Charlotte Py , Lionel Doppler, Paul Reverdy & Charles Baroud
actuation with an electric field: with Miguel Piñeirua

What happens when a water droplet is deposited on a flexible sheet? Does the sheet spontaneously wrap the droplet? Yes, if driving capillary forces overtake the elastic bending resistance of the sheet. If the sheet is stiffer, the corners start bending but the sheet quickly reopens.
The final conformation is dictated by the initial cut of the sheet. Pyramids, cubes or quasi-spheres are obtained from triangles, crosses or flowers shapes, respectively. Beyond scientific curiosity, we believe this capillary origami mechanism to be relevant for building three dimensional micro-structures from two dimensional templates. At small scales capillary forces dominate and minute droplets may serve as micro-pliers.
The opening and closure of the structure can finally be actuated by an electric field applied between the droplet and the ground.
Soft Matter 6, 4491 (2010)
The European Physical Journal Special Topics 166, 67 (2009)
Physical review letters 98, 156103 (2007)

Wrapping a sphere with a sheet
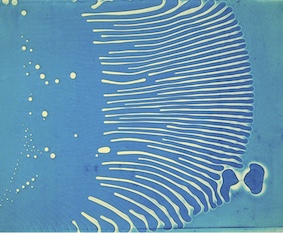
with Jérémy Hure & Benoît Roman

Can we wrap a sphere with an adhesive sheet? Cartographers know from centuries that it is not possible to provide a planar representation of the earth without stretching the continents. This geometrical constraint results from the theorema egregium from the mathematician Gauss. As a consequence the contact zone between the adhesive sheet and the sphere adopts a complex morphology depending on the bending and stretching rigidities of the sheet. If the sheet is thin enough, we observe a ramified oscillatory shape.
Physical Review Letters 106, 174301 (2011)

Adhesion of a soft cap on a rigid sphere
with Hadrien Bense, Marie Tani, Maïka Saint Jean,Étienne Reyssat & Benoît Roman

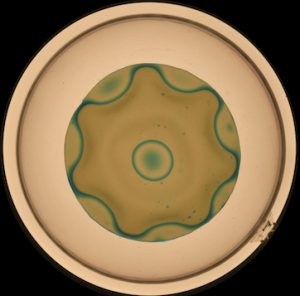
Soft contact lenses are sold with discrete sizes, which generally do not perfectly fit the curvatures of patiens’ eyes. Within which conditions such mismatch may be accomodated? We determine the maximum size of the lense that lead to perfect contact for a given difference in curvature and show a large variety of adhesion patterns beyond this critical size.

Soft Matter 16, 1961 (2020)

Capillary buckling of a floating annulus
with Miguel Piñeirua, Nana Tanaka & Benoît Roman

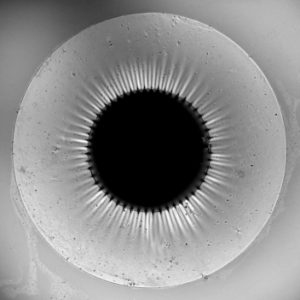
Can surfactant molecules induce wrinkles in a floating sheet?
Out-of-plane buckling of a flexible annulus floating on a bath of water is observed as surfactant molecules are added outside the annulus. The difference in surface tension induces compressive stresses, which result in regular orthoradial wrinkles beyond a critical difference in surface tension. The wrinkles first appear in the vicinity of the inner edge of the annulus and progressively grow as the concentration of surfactant is increased. Conversely, the wavenumber remains constant and relies on a simple balance between gravity and the bending stiffness of the membrane within the range of our experimental parameters.
Soft Matter 9, 10985 (2013)

Interfaces & Instabilités / Interfaces & Instabilities

Fingering instability in adhesion fronts
with Manon L’Estimé, Laurent Duchemin & Etienne Reyssat

 The adhesion of two surfaces relies on the propagation of an adhesion front. What is the dynamics of the front when both surfaces are coated with a thin layer of viscous liquid? Standard criteria from fingering instabilities would predict a stable front since viscous fluid pushes away air of low viscosity. Surprisingly, the front propagation may be unstable and generally leads to growing fingers. We demonstrate with model experiments where the two adhering surfaces are slightly tilted that the origin of this interfacial instability relies on feeding the front from the surrounding thin film. We show experimentally that the typical wavelength of the instability is mainly dictated by the thickness of the oil layers. In this wedge geometry, the propagation dynamics is found to follow a t½ dependence and to saturate for an extension length of the order of the ratio of the film thickness with the wedge angle.
Journal of Fluid Mechanics 949, A46 (2022)

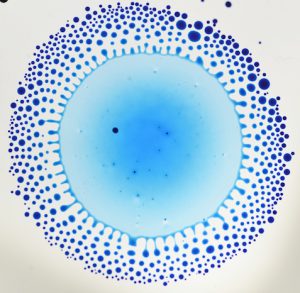
Marangoni bursting
with Ludovic Keiser, Hadrien Bense, Pierre Colinet & Etienne Reyssat

A drop of water and volatile alcohol deposited on a bath of oil spreads and spontaneously fragments into a myriad of minute droplets. The size of the expelled droplets strongly depends on the initial concentration of alcohol. Marangoni flows induced by the evaporation of alcohol play a key role in the overall phenomenon. The intricate coupling of hydrodynamics, wetting, and evaporation is well captured by analytical scaling laws.
This experiment was first introduced to us by Gustavo Gutiérrez from U. Simon Bolivar, Venezuela, who has been presenting it for years to school kids from Caracas in science festivals.

Click on the image to see the movie edited with Guillaume Durey & Hoon Kwon from Lutetium Project.
Physical Review Letters 118, 074504 (2017)

Capillary instabilities in wedges
with Ludovic Keiser, Rémy Herbaut & Étienne Reyssat

How can oil be extracted for a confined region? We present an experiment where oil is first trapped in a wedge is spontaneously washed away by a more wetting liquid (a surfactant solution) through a capillary instability. Regular fingers progressively grow and droplets pinch off. They are eventually driven away from the apex of the wedge by surface tension.
Journal of Fluid Mechanics 790, 619 (2016)
Journal of Fluid Mechanics 845, 245 (2018)

Gobbling droplets
with Christian Clasen, Gareth McKinley & Vladimir Entov

A jet of liquid is unstable because of surface tension and usually breaks into small droplets. The addition of minute quantities of polymeric molecules provides an additive elastic stress which stabilizes the liquid column. In this situation the terminal droplet has the time to gobble many of its incoming neighbors before its detachment.
Journal of fluid mechanics 636, 5 (2009)

Rolling Stones
with Jacqueline Ashmore, Howard Stone & Gareth McKinley

Once deposited on a tilted planar surface coated with some viscous liquid, a sphere rolls down and slides at the same time. Tire prints like patterns are formed behind the ball. An overhang situation is also possible: an heavy ball rolls down eventually without falling off, only hold by a liquid bridge!
Physics of fluids 21, 082103 (2009)

Super Hydrophobic / Hydrophilic Surfaces
initially with David Quéré & Denis Richard, later with G. McKinley, K.Lau, K.B.K. Teo, M. Chhowalla, G.A.J. Amaratunga and W.I. Milne

The combination of an hydrophobic material and and rough surface can lead to super hydrophobic surfaces. A water droplet deposited on such a substrate remains at rest on the tops of the roughness which widely reduces the contact area of the liquid with the solid. The drop is mainly in contact with air and keeps the shape it would have in the air.
Conversely, a wetting liquid imbibes the roughness, This super wetting effect is interesting for anti-fogging materials.
Nano Letters 3, 1701 (2003)
Nanotechnology 14, 1109 (2003)
Europhysics Letters 61, 348 (2003)
Colloids and Surfaces A 206, 41 (2002)
Europhysics Letters 55, 214 (2001)
Europhysics Letters 47, 220 (1999)

Liquid trains in a tube
with David Quéré

If two adjacent liquids are introduced in a capillary tube, a spontaneous motion of this liquid train is generally observed when the tube is hold horizontally. This flow relies on the asymmetry of the system: capillary forces on the three menisci do not necessarily balance and their contrast drives the bislug.
This motion is not perpetual since a trail of the liquids is left behind the train which is consumed during its displacement.
Europhysics Letters 51, 546 (2000)
Journal of colloid and Interface Science 243, 262 (2001)
Journal of colloid and Interface Science 247, 162 (2002)
Journal of Fluid Mechanics 467, 101 (2002)