Out in Nature, our work on DNA-encoded neural networks powered by enzymes. I think it deserves a summary article:

Being able to compute at the molecular level, leveraging the high parallelization and energy-efficiency of (bio)chemical reactions, will enable to build low-tech, accurate molecular classifiers for diagnosis (more to come soon !) or to interact with DNA-stored databases (e.g. https://www.softwareheritage.org/2022/06/28/all-of-humankinds-source-code-in-a-nutshell/).

DNA is the perfect medium for that task: high predictability of strand interactions (A with T, G with C you know the story); cheap (cheaper and cheaper); directly compatible with a bunch of biomarkers for diagnosis. From the in silico world, artificial neural networks (ANN) have percolated in molecular medicine and are proven relevant to classify for instance cancer patients from healthy individuals. Why not using DNA to encode the algorithm of the ANN and perform the computation directly in a tube on the biomarker inputs ?

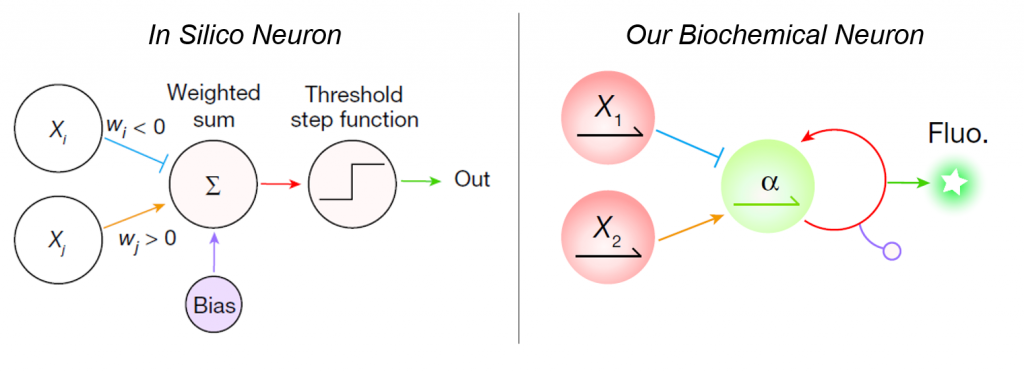
A few papers in this direction have been seminal to the field of DNA computing [1-3]. In these influential proofs of principle, only DNA is used, and computation relies solely on DNA (de)hybridization.

In our work, we exploit another advantage of using DNA: the myriad enzymes that can tinker with it (polymerase to write DNA, exonuclease to erase DNA, endonucleases to cut and edit DNA…). I’ll pass on the comparison of DNA-only versus DNA-enzyme networks, available in the supplementary information. But how does our molecular neural network works:

The connectivity of the network is provided by short DNA strands that we call templates, which encode all elementary functions of a neural net:

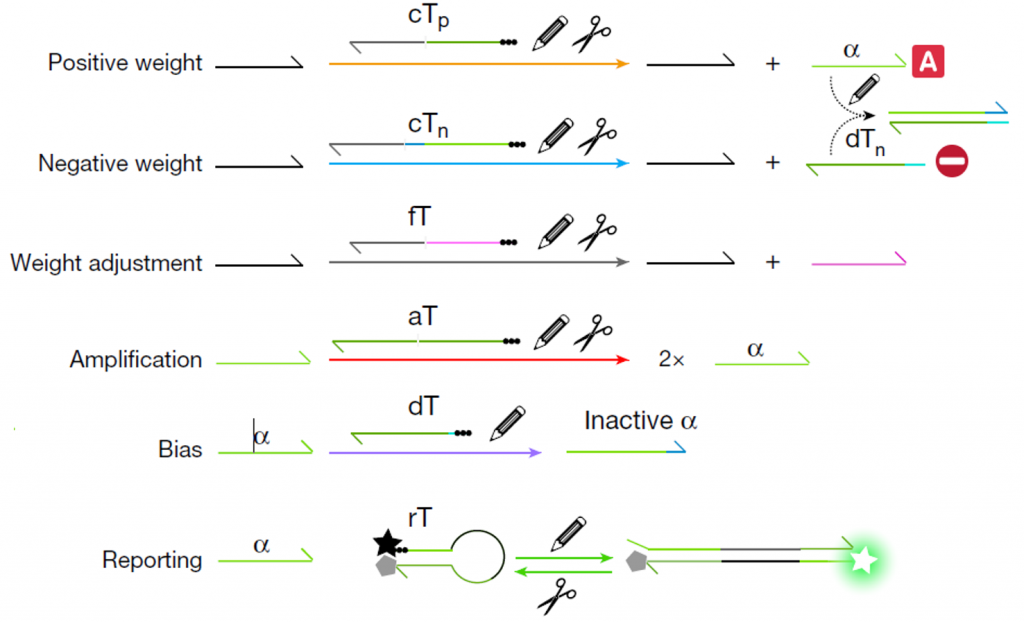
  • Positive and negative weights convert the input into an activator or an inhibitor of a DNA neuron, respectively.
  • Weights can be independently adjusted by adding another template to control the rate of production of activators and inhibitors.
  • The activation function is encoded in an autocatalytic template that initiate the exponential amplification of the output strand if and only if a given ratio of activator/inhibitor is exceeded.
  • The bias of each neuron can also be tuned by another template that absorb a fraction of activator.
  • A DNA neuron can have an optical output using… a reporter template that uses the output strand to generate a fluorescence signal.

Three types of enzymes are at play to catalyze the reactions: DNA polymerase, exonuclease and endonucleases (two nicking enzymes to be precise)

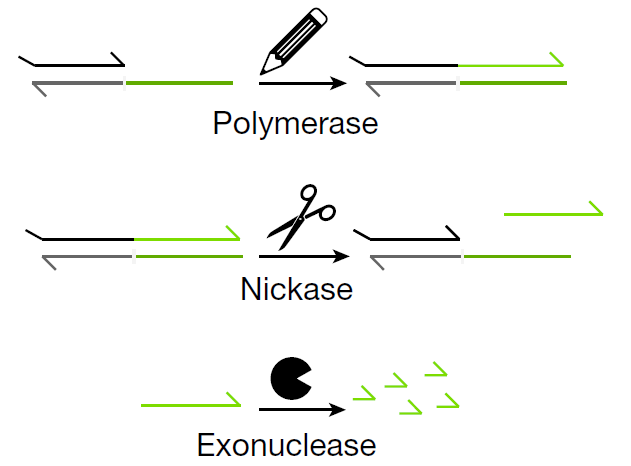
Now that we have all ingredients of a DNA-neuron, let’s build neural networks !

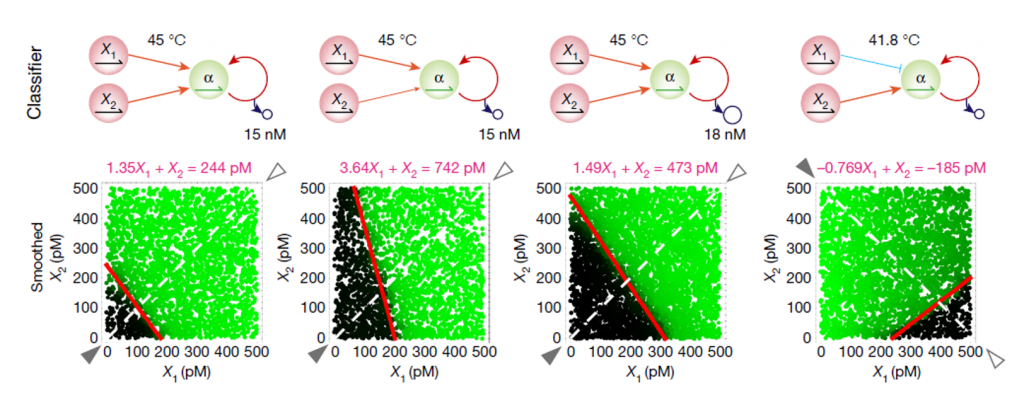
With a single layer, we build a series of perceptron-like linear classifiers based on two microRNA sequence inputs (at picomolar to subnanomolar concentrations). Importantly, the expertise of the DNAgroup (LIMMS Tokyo) in microfluidics was used to create picoliter droplets and parallelized the computation on dozens of thousands of experimental conditions (input combinations and temperature for instance, [4]).

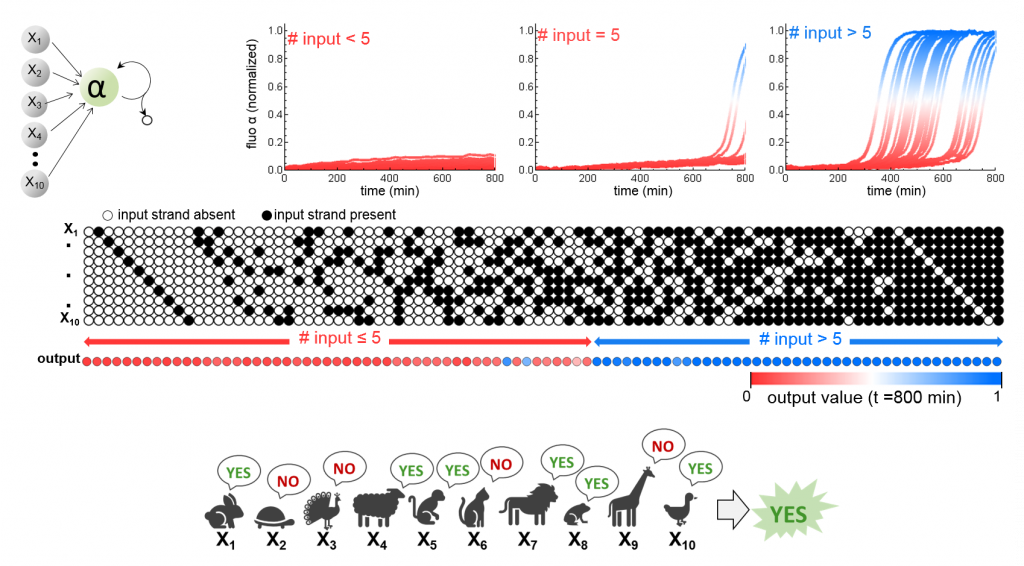
Upon the same principle, we implemented a majority voting algorithm on 10 inputs strands (all with the same weight). Amusingly, we can arbitrarily attribute an input a veto right (negative output whatever the number of positive votes) or a majority power (positive output even if everybody else votes against).

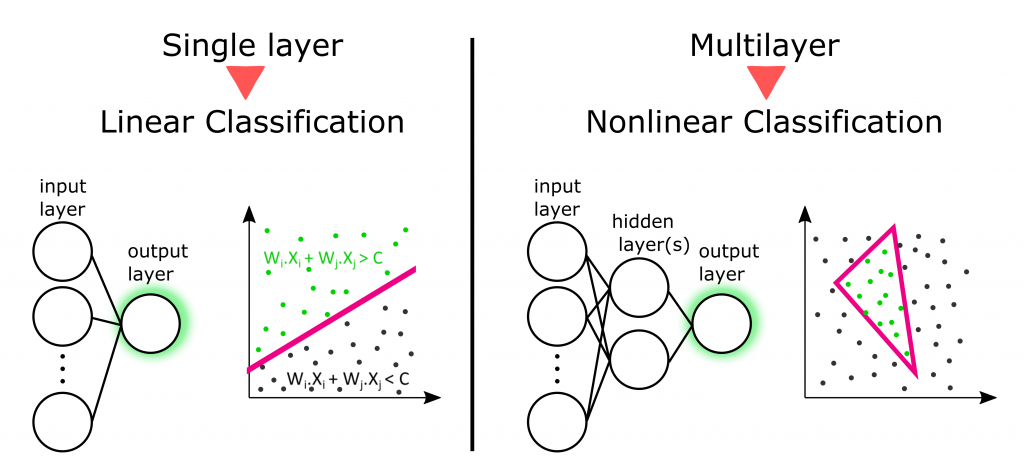
Again, single-layer allows to classify only linearly separable data (basically, to draw a line in 2D data line the microRNA classifier mentioned above). Nonlinear classification involves at least two layers.

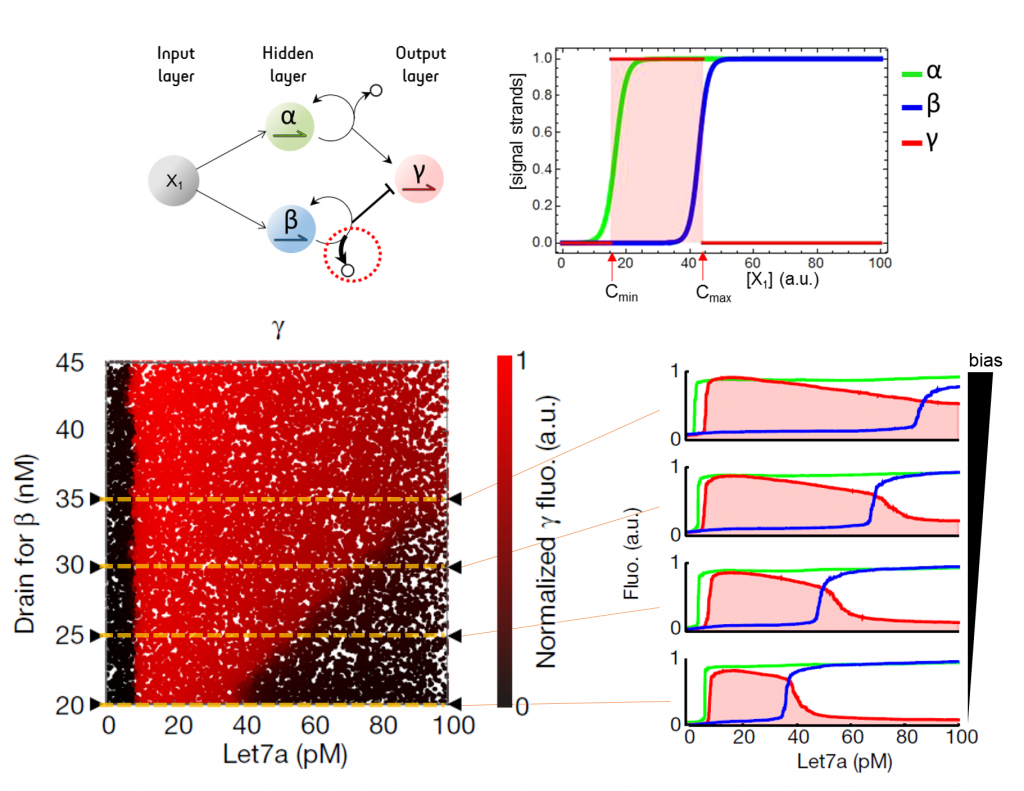
So we assembled 1 input layer (1 neuron), 1 hidden layer (2 neurons) and 1 output layer (1 neuron, which has a red fluorescence output) and connected them so that the network encodes a gate (or rectangular) function: the output neuron is OFF at low (< Cmin) and high (> Cmax)  concentrations of the input (the microRNA let-7a) and ON at intermediate concentrations between Cmin and Cmax. We show that we can tune the bias of a neuron of the hidden layer to adjust Cmax, and therefore tune the width of the gate.

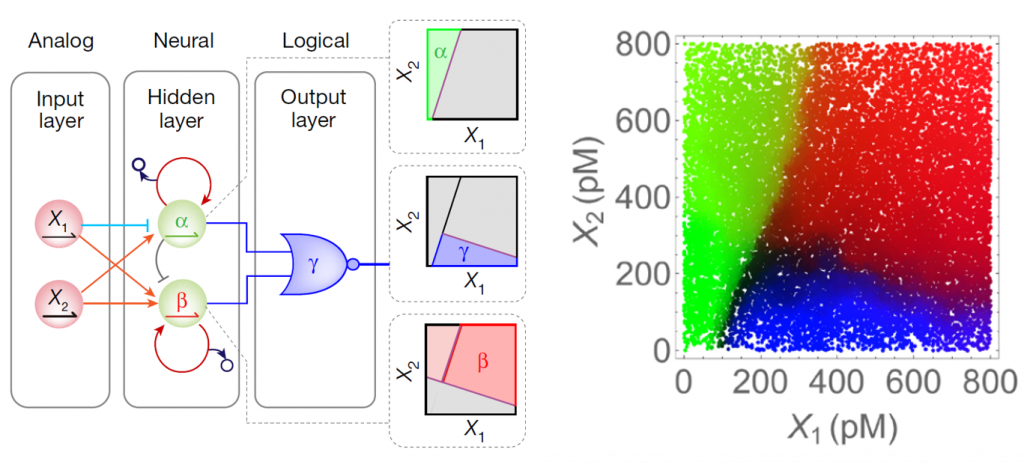
Finally, we created a decision tree encoded in a fully connected hybrid network (with 1 hidden layer and 1 logic output gate). The network robustly partitions the 2D concentration plane into 3 nonlinearly separable region.

What are the next step ? Well, while we’ve shown we can create enzymatic neural networks, it remains the tricky question of the training: how can we make a network learn the weight to achieve a given classification task.

Finally, one dream goal is to have these networks implemented in real-world applications. Let’s imagine such DNA-enzyme classifier, capable of recognizing a cancer molecular signature from a blood sample. Still a couple of milestones to reach… but let’s imagine.

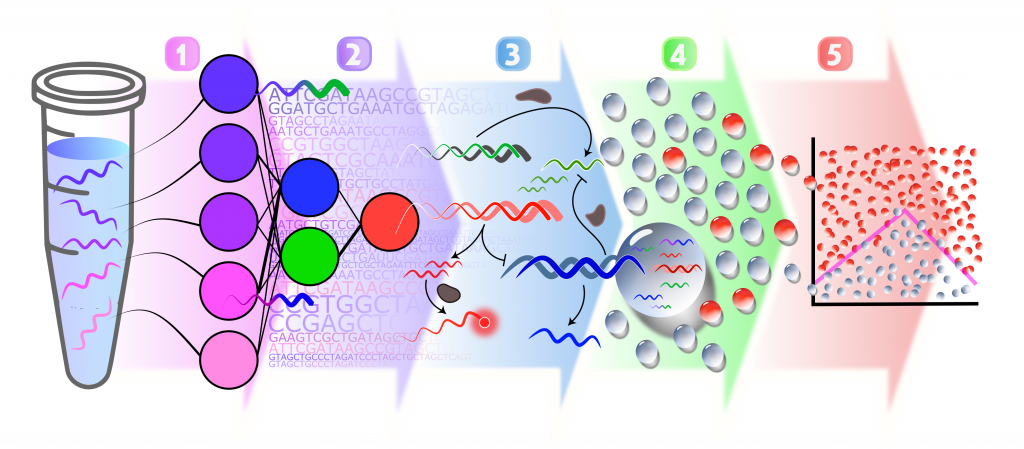
From left to right: A molecular signature (purple and pink DNA strand) is recognized by an artificial neural network (1). This architecture is encoded in molecular network composed of DNA templates (2). The computation is powered by 3 enzymes (DNA polyemrase, nicking enzyme and exonuclease) that catalyse the production and degradation of DNA signal that transit between layers. In fine, a red fluorescence output is generated if the molecular signature is recognized (3). This type of computation can be operated in parallel in dozens of thousands of microfluidic droplets, each computing on a different combination of input strand concentrations (4). The output fluorescence of each droplet is indexed to its content, revealing the result of the classification (5)

This work is part of the Objective 2 of the ERC project MoP-MiP.

Nonlinear decision-making with enzymatic neural networks, S. Okumura, G. Gines, N. Lobato-Dauzier, A. Baccouche, R. Deteix, T. Fujii, Y. Rondelez & A. J. Genot, Nature, 2022

References:
(1) Lopez, R.; Wang, R.; Seelig, G. A Molecular Multi-Gene Classifier for Disease Diagnostics. Nature Chemistry 2018, 10 (7), 746.
(2) Cherry, K. M.; Qian, L. Scaling up Molecular Pattern Recognition with DNA-Based Winner-Take-All Neural Networks. Nature 2018, 559 (7714), 370.
(3) Zhang, C.; Zhao, Y.; Xu, X.; Xu, R.; Li, H.; Teng, X.; Du, Y.; Miao, Y.; Lin, H.; Han, D. Cancer Diagnosis with DNA Molecular Computation. Nature Nanotechnology 2020, 1–7.
(4) Genot, A. J.; Baccouche, A.; Sieskind, R.; Aubert-Kato, N.; Bredeche, N.; Bartolo, J. F.; Taly, V.; Fujii, T.; Rondelez, Y. High-Resolution Mapping of Bifurcations in Nonlinear Biochemical Circuits. Nature Chemistry 2016, 8 (8), 760–767.