Auteur/autrice : Benoît Roman

Our book will be translated and published by MIT press in February 2021 « Hidden Wonders : the subtle dialogue between physics and elegance »

See also our blog in English (in construction) : hidden wonders

You can already see the cover, and the description on MIT Press website.

A detailed article in JMPS « Geometry and mechanics of inextensible curvilinear balloons« on the shape of inextensible curvilinear balloon obtained when sealing along their edges two identical flat pieces of intextensible membranes.

Abstract

Mylar balloons are popular in funfairs or birthday parties. Their conception is very simple: two pieces of flat thin sheets are cut and sealed together along their edges to form a flat envelope. Inflation tends to deform this envelope in order to maximize its inner volume. However, although thin sheets are easy to bend and hardly resist compressive loads, they barely stretch, which imposes non-trivial geometrical constraints. Such thin sheets are generally described under the framework of “tension field theory” where their stiffness is considered as infinite under stretching and vanishes under compression or bending.

In this study, we focus on the shape after inflation of flat, curved templates of constant width. Counter-intuitively, the curvatures of the paths tend to increase upon inflation, which leads to out of plane buckling of non-confined closed structures. After determining the optimal cross section of axisymmetric annuli, we predict the change in local curvature induced in open paths. We finally describe the location of wrinkled and smooth areas observed in inflated structures that correspond to compression and tension, respectively.

https://doi.org/10.1016/j.jmps.2020.104068

We report a new oscillatory propagation of cracks in thin films where three cracks interact mediated by two delamination fronts. Experimental observations indicate that delamination fronts joining the middle crack to the lateral crack tips swap contact periodically with the crack tip of the middle crack. A model based on a variational approach analytically predicts the condition of propagation and geometrical features of three parallel cracks. The stability conditions and oscillating propagation are found numerically and the predictions are in favorable agreement with experiments. We found that the physical mechanism selecting the wavelength structure is a relaxation process in which the middle crack produces a regular oscillatory path.

Collaborative Oscillatory Fracture

Juan-Francisco Fuentealba, Joel Marthelot, Benoît Roman, and Francisco Melo

Phys. Rev. Lett. 124, 174102 (2020) – Published 30 April 2020

We have shown that the spiraling path (when a cone is pushed through a brittle sheet) and the oscillatory crack path (when a blunt object tears through a brittle sheet) both result from the same instability.

Cutting a brittle thin sheet with a blunt object leaves an oscillating crack that seemingly violates the principle of local symmetry for fracture. We experimentally find that at a critical value of a well chosen control parameter the straight propagation is unstable and leads to an oscillatory pattern whose amplitude and wavelength grow by increasing the control parameter. We propose a simple model that unifies this instability with a related problem, namely that of a perforated sheet, where through a similar bifurcation a series of radial cracks spontaneously spiral around each other. We argue that both patterns originate from the same instability.

See the article here in Physical Review Letters

Nature of Crack Path Instabilities in Thin Sheets Cut by Blunt Objects

Eugenio Hamm, Iryna Sivak, and Benoît Roman

Phys. Rev. Lett. 124, 174101 – Published 29 April 2020

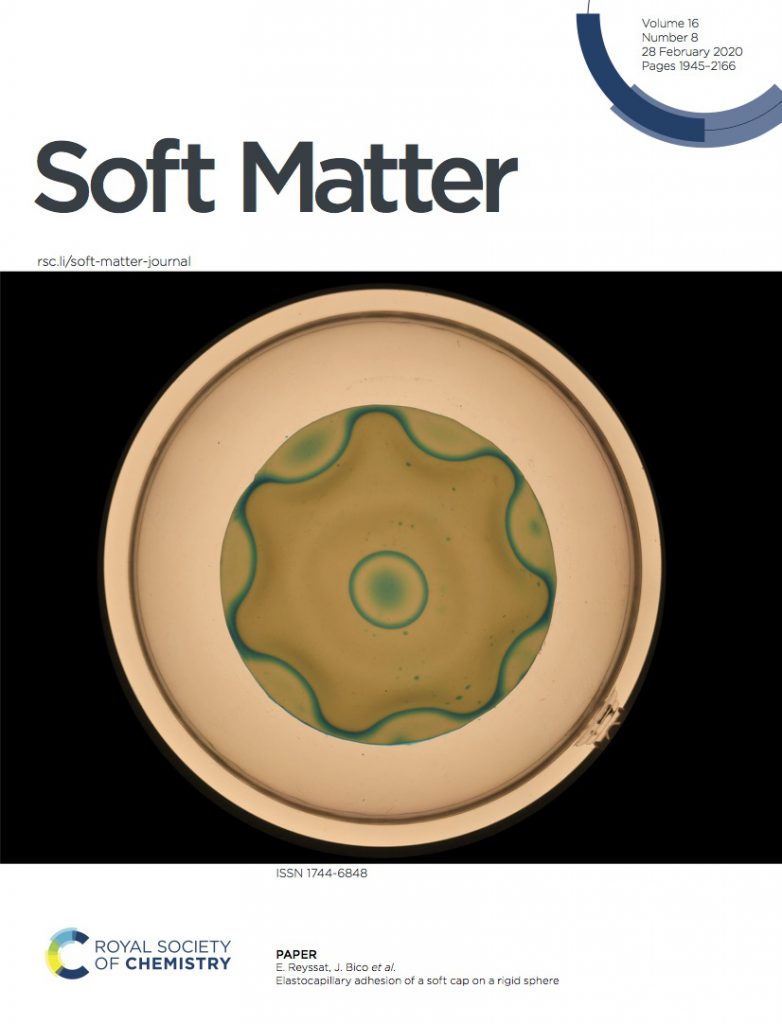
Here is the link to the article Elastocapillary adhesion of a soft cap on a rigid sphere

The capillary adhesion of soft shells on spheres of different curvature gives rise to a family of complex adhesion patterns.

---

The article was first published on 22 Jan 2020
Soft Matter, 2020,16, 1961-1966
https://doi.org/10.1039/C9SM02057H

Inflatable structures are flat and foldable when empty and both lightweight and stiff when pressurized and deployed. They are easy to manufacture by fusing 2 inextensible sheets together along a defined pattern of lines. However, the prediction of their deployed shape remains a mathematical challenge, which results from the coupling of geometrical constraints and the strongly nonlinear and asymmetric mechanical properties of their composing material: thin sheets are very stiff on extensional loads, while they easily shrink by buckling or wrinkling when compressed. We discuss the outline shape, local cross-section, and state of stress of any curvilinear open path. We provide a reverse model to design any desired curved 2-dimensional shape from initially flat tubes.

See our article in PNAS and the Supplementary Information.