ESPCI web site
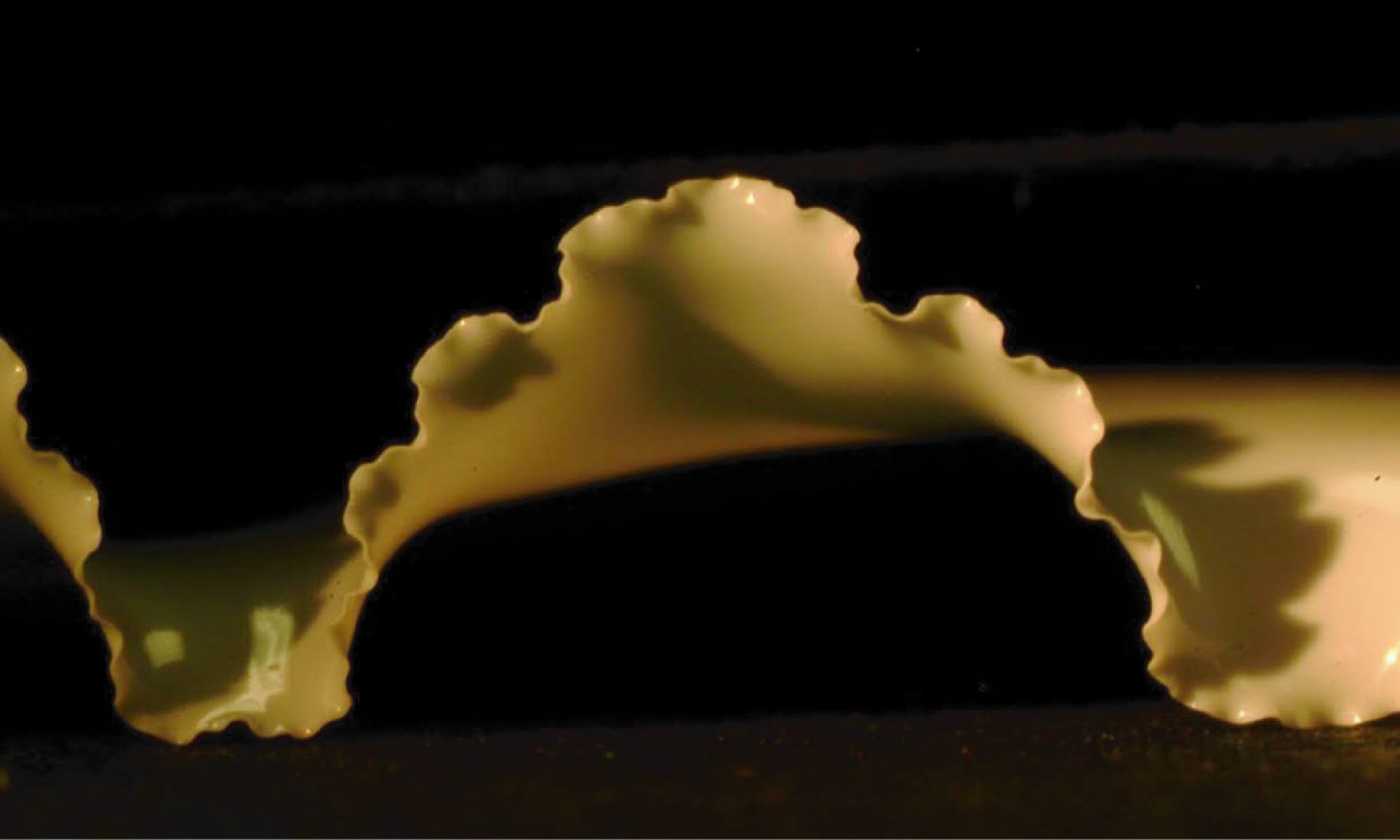
Les structures minces sont souvent considérées comme quasi-inextensibles, ce qui leur pose de sérieux problèmes de géométrie.
En effet, le théorème de Gauss (theorema egregium) impose que si les distances le long d’une surface (la métrique) sont conservées, alors la surface doit conserver sa courbure de Gauss (le produit des deux courbures principales).
Si les conditions imposées tendent à imposer une courbure de Gauss non-nulle, la réponse d’une plaque initialement plane va donc se révéler très complexe : flambage, singularités de froissement…
Pour produire des changement de forme important (par exemple pour transformer ne serait-ce qu’une plaque en calotte sphérique), il faut donc altérer la métrique, c’est à dire la distance naturelle entre les points d’une plaque.
Instabilités Electro-actives, et surfaces à changement de forme.
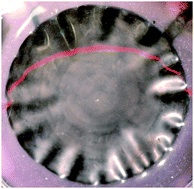Les élastomères electro-actifs, de déforment augmente lorsqu’ils sont soumis à une différence de potentiel électrique (déformation inélastique membranaire). Lorsque ces pré-contraintes compressives ne sont pas uniformes, une incompatibilité donne lieu à une instabilité de flambage. Peut-on utiliser cet effet pour modifier la métrique d’une plaque et programmer des formes tri-dimensionnelles ?
Emboutissage et plissement.
Froissement et défroissement
