Catégorie : Publication

Nous avons participé à un beau livre collectif qui est sorti le 9 septembre 2022 (Edition B42)

Il y est question de Quotidien et de Plis (nos entrées)

Qu’est-il advenu de la beauté ? Du charme dissimulé dans le quotidien au régime esthétique atypique de l’imagerie scientifique, de sa capacité inouïe à penser le vivant jusqu’à ses innombrables applications littéraires, philosophiques, techniques, historiques et artistiques, la beauté se révèle être un terrain intellectuel particulièrement fécond.

Cet abécédaire croise les axes de réflexion autour d’une notion aussi galvaudée qu’insaisissable, mais qui, selon les quarante-trois contributions réunies ici, demeure au centre de nos préoccupations les plus actuelles et les plus vives. Mêlant à la fois une réflexion sur les termes attendus (Grèce, Style, Sublime, Vénus) et d’autres beaucoup plus insolites (Déchets, Robot, Chaos, Pieuvre), la beauté est présente comme un cadre structurant nos pensées mais également comme une lézarde, diffuse et souterraine, dans les interstices de toutes nos modalités d’existence.

Sous la direction de Clélia Zernik et Justin Jaricot.
Illustrations par Icinori.

où le trouver ? ici ou dans une librairie près de chez vous : place des librairies

Our book is available, starting February 23rd 2021 !

The hidden elegance in everyday objects and physical mechanisms, from crumpled paper to sandcastles.

Hidden Wonders focuses on the objects that populate our everyday life—crumpled paper, woven fabric, a sand pile—but looks at them with a physicists’ eye, revealing a hidden elegance in mundane physical mechanisms. In six chapters—Builders, Creating Shapes, Building with Thread, From Sand to Glass, Matter in Motion, and Fractures—the authors present brief stories, set in locales ranging from the Eiffel Tower to a sandcastle, that illustrate the little wonders hidden in the ordinary. A simple experiment that readers can perform at home concludes each story. More than 200 illustrations bring the stories to life.

Through these stories and images, the authors explain the amazing mechanisms that govern the elements that surround us, offering a close look at the subtle dialogue of form, force, and function. They connect the underlying physics to a range of applications: crumpled graphene sheets that may be used in batteries, wet-hair physics that must be taken into account in the manufacturing of mechanical microdevices, pine cone mechanisms used in contemporary architecture, and more. Each chapter offers striking two-page spreads of text and images.

Endorsements

How everyday objects reflect deep and beautiful mathematics and physics. You'll never look at a bubble, a spider's web, or a wineglass in quite the same way again. Utterly fascinating!

Ian Stewart, author of Do Dice Play God?, Calculating the Cosmos, and The Beauty of Numbers in Nature

Hidden Wonders is a lovely reminder that amazing science needn’t be exotic or remote, but surrounds us every day with riches at the same time reassuringly familiar and constantly surprising.”

Philip Ball author of Patterns in Nature, Beyond Weird, and The Beauty of Chemistry: Art, Wonder, and Science

From why things break to why they hold together, from why cut flowers wilt to why arches can stand for centuries, from the drape of a necklace to the strength of sea shells, Hidden Wonders is endlessly entertaining and enlightening. With clear prose, engaging illustrations and kitchen-table do-at-home experiments, this fun and accessible book will give you a new appreciation for the wonders of the world—both natural and man-made—that surround us every day.

James Kakalios Professor of Physics, University of Minnesota; author of The Physics of Superheroes and The Physics of Everyday Things

Emmanuel Siéfert, Etienne Reyssat, José Bico and Benoît Roman

Origami-inspired design of Gaussian morphing fabrics structures. Superimposed flat and inextensible fabric sheets are heat-sealed along a specific pattern of lines. Upon inflation, this network of tubular cavities deploys into a large, stiff and light shell, with a programmed shape.

---

Soft Matter, 2020,16, 7898-7903
https://doi.org/10.1039/D0SM01041C

Our book will be translated and published by MIT press in February 2021 « Hidden Wonders : the subtle dialogue between physics and elegance »

See also our blog in English (in construction) : hidden wonders

You can already see the cover, and the description on MIT Press website.

A detailed article in JMPS « Geometry and mechanics of inextensible curvilinear balloons« on the shape of inextensible curvilinear balloon obtained when sealing along their edges two identical flat pieces of intextensible membranes.

Abstract

Mylar balloons are popular in funfairs or birthday parties. Their conception is very simple: two pieces of flat thin sheets are cut and sealed together along their edges to form a flat envelope. Inflation tends to deform this envelope in order to maximize its inner volume. However, although thin sheets are easy to bend and hardly resist compressive loads, they barely stretch, which imposes non-trivial geometrical constraints. Such thin sheets are generally described under the framework of “tension field theory” where their stiffness is considered as infinite under stretching and vanishes under compression or bending.

In this study, we focus on the shape after inflation of flat, curved templates of constant width. Counter-intuitively, the curvatures of the paths tend to increase upon inflation, which leads to out of plane buckling of non-confined closed structures. After determining the optimal cross section of axisymmetric annuli, we predict the change in local curvature induced in open paths. We finally describe the location of wrinkled and smooth areas observed in inflated structures that correspond to compression and tension, respectively.

https://doi.org/10.1016/j.jmps.2020.104068

We report a new oscillatory propagation of cracks in thin films where three cracks interact mediated by two delamination fronts. Experimental observations indicate that delamination fronts joining the middle crack to the lateral crack tips swap contact periodically with the crack tip of the middle crack. A model based on a variational approach analytically predicts the condition of propagation and geometrical features of three parallel cracks. The stability conditions and oscillating propagation are found numerically and the predictions are in favorable agreement with experiments. We found that the physical mechanism selecting the wavelength structure is a relaxation process in which the middle crack produces a regular oscillatory path.

Collaborative Oscillatory Fracture

Juan-Francisco Fuentealba, Joel Marthelot, Benoît Roman, and Francisco Melo

Phys. Rev. Lett. 124, 174102 (2020) – Published 30 April 2020

We have shown that the spiraling path (when a cone is pushed through a brittle sheet) and the oscillatory crack path (when a blunt object tears through a brittle sheet) both result from the same instability.

Cutting a brittle thin sheet with a blunt object leaves an oscillating crack that seemingly violates the principle of local symmetry for fracture. We experimentally find that at a critical value of a well chosen control parameter the straight propagation is unstable and leads to an oscillatory pattern whose amplitude and wavelength grow by increasing the control parameter. We propose a simple model that unifies this instability with a related problem, namely that of a perforated sheet, where through a similar bifurcation a series of radial cracks spontaneously spiral around each other. We argue that both patterns originate from the same instability.

See the article here in Physical Review Letters

Nature of Crack Path Instabilities in Thin Sheets Cut by Blunt Objects

Eugenio Hamm, Iryna Sivak, and Benoît Roman

Phys. Rev. Lett. 124, 174101 – Published 29 April 2020

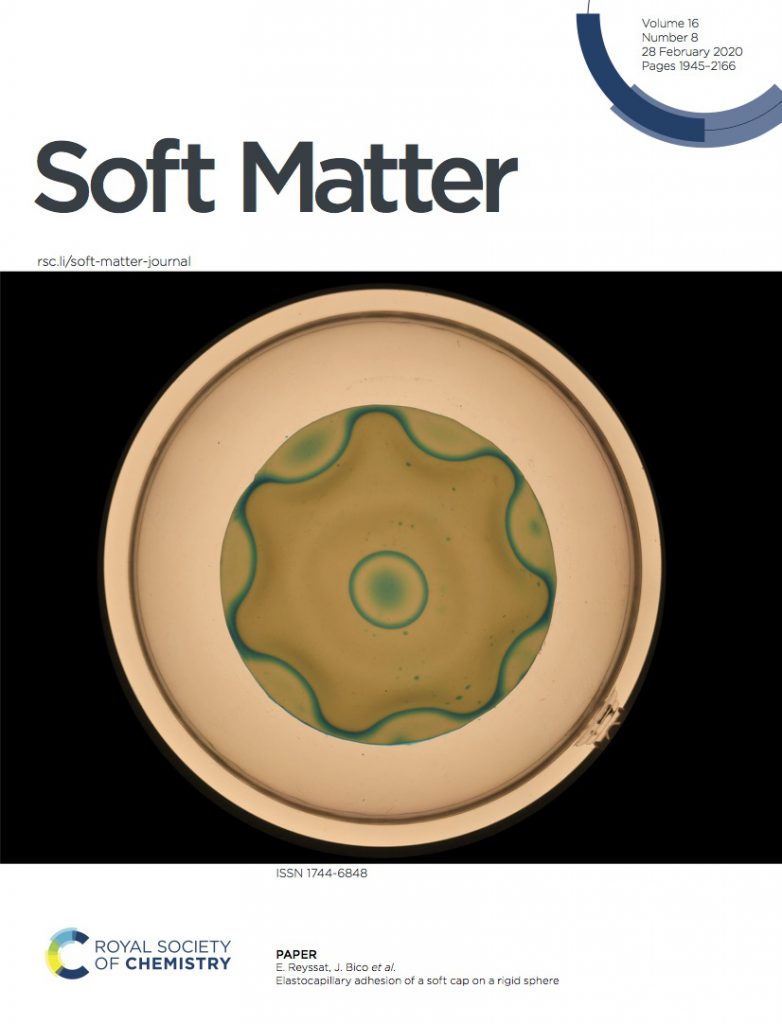
Here is the link to the article Elastocapillary adhesion of a soft cap on a rigid sphere

The capillary adhesion of soft shells on spheres of different curvature gives rise to a family of complex adhesion patterns.

---

The article was first published on 22 Jan 2020
Soft Matter, 2020,16, 1961-1966
https://doi.org/10.1039/C9SM02057H

Inflatable structures are flat and foldable when empty and both lightweight and stiff when pressurized and deployed. They are easy to manufacture by fusing 2 inextensible sheets together along a defined pattern of lines. However, the prediction of their deployed shape remains a mathematical challenge, which results from the coupling of geometrical constraints and the strongly nonlinear and asymmetric mechanical properties of their composing material: thin sheets are very stiff on extensional loads, while they easily shrink by buckling or wrinkling when compressed. We discuss the outline shape, local cross-section, and state of stress of any curvilinear open path. We provide a reverse model to design any desired curved 2-dimensional shape from initially flat tubes.

See our article in PNAS and the Supplementary Information.