ESPCI web site
Quennouz N., Shelley M.J., du Roure, O. & Lindner, A.
Journal of Fluid Mechanics (2015) 769 387- 402
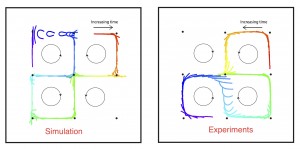
We study, using both experiment and theory, the coupling of transport and shape dynamics for elastomeric fibres moving through an inhomogeneous flow. The cellular flow, created electromagnetically in our experiment, comprises many identical cells of counter-rotating vortices, with a global flow geometry characterized by a backbone of stable and unstable manifolds connecting hyperbolic stagnation points. Our mathematical model is based upon slender-body theory for the Stokes equations, with the fibres modelled as inextensible elastica. Above a certain threshold of the control parameter, the elasto-viscous number, transport of fibres is mediated by their episodic buckling by compressive stagnation point flows, lending an effectively chaotic component to their dynamics. We use simulations of the model to construct phase diagrams of the fibre state (buckled or not) near stagnation points in terms of two variables that arise in characterizing the transport dynamics. We show that this reduced statistical description quantitatively captures our experimental observations. By carefully reproducing the experimental protocols and time scales of observation within our numerical simulations, we also quantitatively explain features of the measured buckling probability curve as a function of the effective flow forcing. Finally, we show within both experiment and simulation the existence of short and long time scales in the evolution of fibre conformation.
Home