Plasticité des amorphes

On utilise un petit modèle simple pour tester des hypothèses quant aux mécanismes de déformation de milieux amorphes ou désordonnés (granulaires, verres métalliques,…). Le désordre est représenté par des seuils de plasticités aléatoires locaux, qui peuvent être activés thermiquement, ou bien lorsque le seuil local est dépassé. Cette déformation plastique locale induit un champ de déformation élastique dans tout le reste du système.

Dans ce modèle, un seul type de déformation est considéré (le cisaillement pur), en considérant qu’il s’agit localement de la déformation d’un petite zone sphérique (transformation d’Eshelby). On calcule la fonction de Green associé à cette déformation, et on l’applique en fonction du site qui est activé. La dynamique est soit une dynamique extrémale (le site le plus faible est activé), soit une dynamique activée thermiquement, en utilisant un algorithme de type Monte-Carlo cinétique, ce qui permet de calculer un temps physique pour un système à température non nulle. On est toujours dans le cas de déformations lentes.

On peut par exemple regarder l’effet d’un vieillissement préalable du système (sans contrainte, mais à une température non nulle), et le comportement lorsqu’on le charge ensuite. On constate dans ce cas que le vieillissement est associé à la localisation de la déformation sous forme de bandes de cisaillement. La déformation peut être suivie soit à charge constante (fluage), soit à taux de déformation imposé.

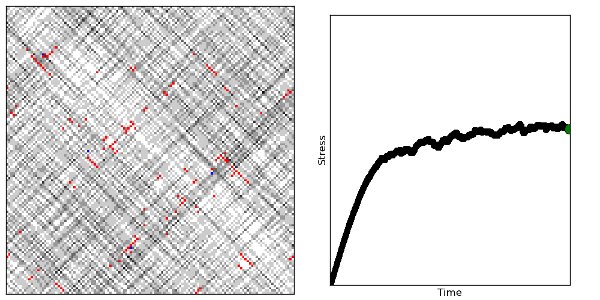
Ci-dessous, des cartes de champs de déformation cumulée, et l’évolution de la contrainte globale en fonction du temps, dans le cas d’un taux de déformation imposé.

Sans vieillissement préalable

Après vieillissement préalable