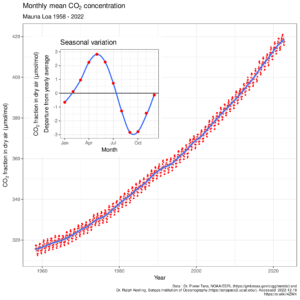
The Keeling curve: arguably one of the most important 2D plots ever?
Recent updates, as well as plots of longer time series, may be found here

The Keeling curve: arguably one of the most important 2D plots ever?
Recent updates, as well as plots of longer time series, may be found here