Here you can find some details about my research interests. I have decided to present only a few of my papers, but you can find a full list of my publications by following the corresponding link.

Tree crowns grow into self-similar shapes controlled by gravity and light sensing (with C. Eloy, E. Badel and B. Moulia)

Plants have developed different tropisms: in particular, they re-orient their branches towards light (phototropism) or upwards (gravitropism). How these tropisms affect the shape of a tree crown remains unanswered. We address this question by developing a propagating front model of tree growth. This model being length-free, it leads to self-similar solutions, independent of the initial conditions, at long time. Varying the intensities of each tropism, different self-similar shapes emerge, including singular ones. Interestingly, these shapes bear similarities with existing tree species. It is concluded that the core of specific crown shapes in trees relies on the balance between tropisms.

Self-similar impulsive capillary waves on a ligament (With Stéphane Le Dizès, Lionel Vincent and Emmanuel Villermaux)

We study the short-time dynamics of a liquid ligament, held between two solid cylinders, when one is impulsively accelerated along its axis. A set of one-dimensional equations in the slender-slope approximation is used to describe the dynamics, including surface tension and viscous effects. An exact self-similar solution to the linearized equations is successfully compared to experiments made with millimetric ligaments. Another non-linear self-similar solution of the full set of equations is found numerically. Both the linear and non-linear solutions show that the axial depth at which the liquid is affected by the motion of the cylinder scales like √tt, a consequence of the imposed radial uniformity of the axial velocity at the cylinder surface, and differs from t2/3t2/3 known to prevail in surface-tension-driven flows. The non-linear solution presents the peculiar feature that there exists a maximum driving velocity U⋆U⋆ above which the solution disappears, a phenomenon probably related to the de-pinning of the contact line observed in experiments for large pulling velocities.

• Self-similar impulsive capillary waves on a ligament (PDF)
  L. Duchemin, S. Le Dizès, L. Vincent & E. Villermaux, 2015, To appear in Physics of Fluids,

Impact on a floating elastic membrane (With Nicolas Vandenberghe)

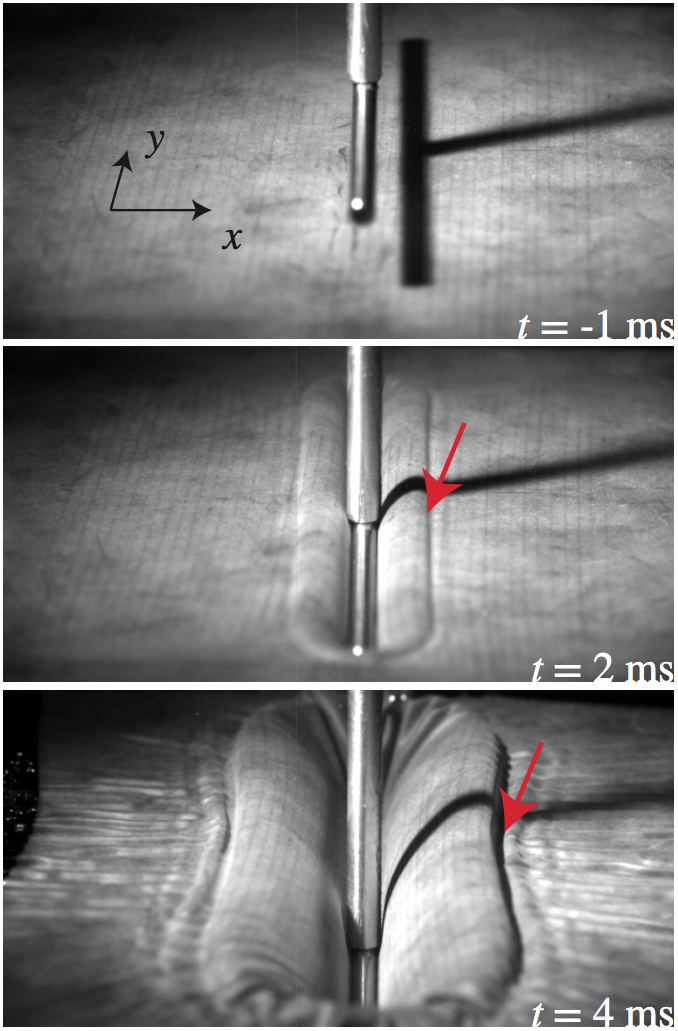
We study impacts of a rigid body on a thin elastic sheet floating on a liquid. When struck by a solid object of small size, the elastic sheet deforms and waves propagate in and on the membrane. The impact triggers a longitudinal elastic wave effectively stretching the membrane. The hydro-elastic transverse wave that propagates in the stretched domain is similar to capillary waves on a free surface with an equivalent surface tension” that results from the stretching of the elastic membrane. Two limiting cases, for which a self-similar solution can be computed, corresponding to short and long times are identified. Surprisingly, our study reveals that the fluid-body system behaves as a regular liquid-gas interface, but with an effective surface tension coefficient that scales linearly with the impact velocity.

• Impact dynamics for a floating elastic membrane (PDF)
  L. Duchemin & N. Vandenberghe, 2014, J. Fluid Mech., vol. 756, 544–554.

The Explicit-Implicit-Null method (With Jens Eggers)

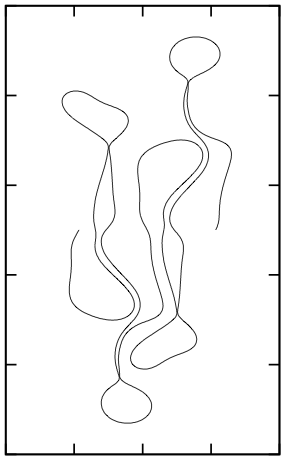
A general method to remove the numerical instability of partial differential equations is presented. Two equal terms are added to and subtracted from the right-hand-side of the PDE~: the first is a damping term and is treated implicitly, the second is treated explicitly. A criterion for absolute stability is found and the scheme is shown to be convergent. The method is applied with success to the mean curvature flow equation, the Kuramoto–Sivashinsky equation, and to the Rayleigh–Taylor instability in a Hele-Shaw cell, including the effect of surface tension.

• The Explicit-Implicit-Null method: removing the numerical instability of PDEs (PDF)
  L. Duchemin & J. Eggers, 2014, J. Comput. Phys., vol. 263, 37-–52.
• Link

Drop impact (With Christophe Josserand)

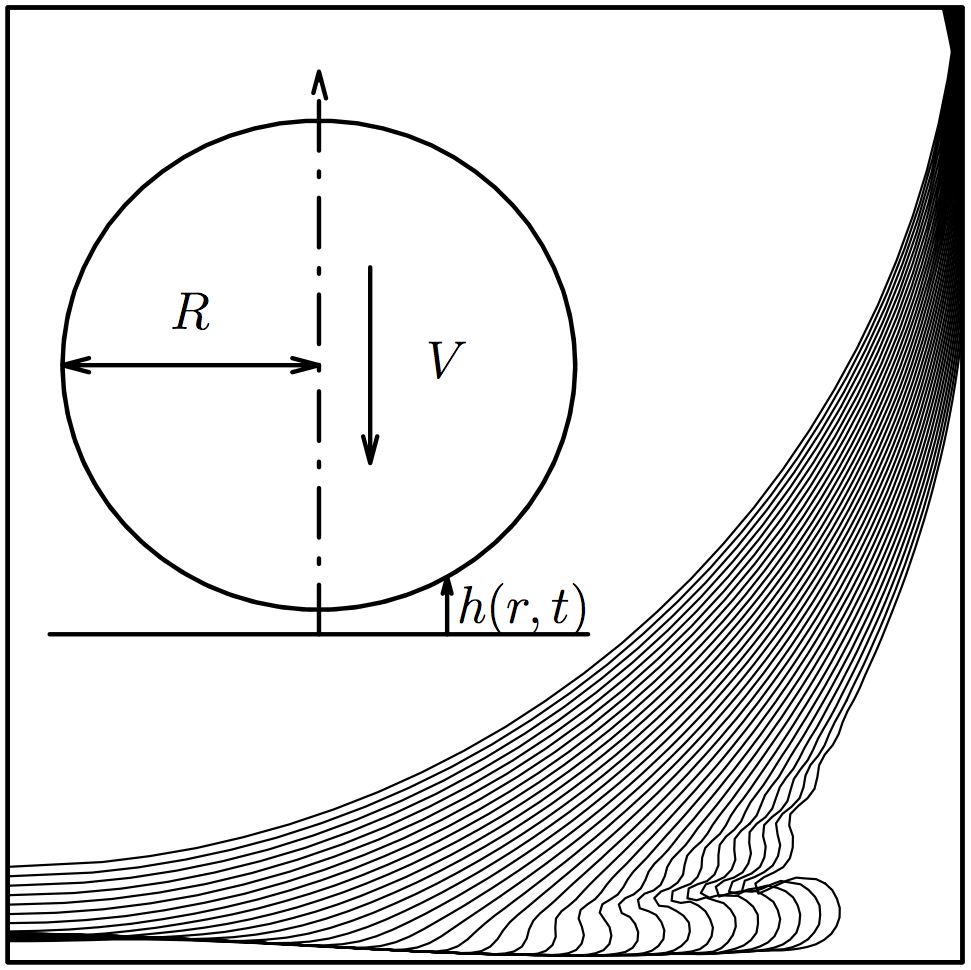
We study the influence of the surrounding gas in the dynamics of drop impact on a smooth surface. We use an axisymmetric model for which both the gas and the liquid are incompressible; lubrication regime applies for the gas film dynamics and the liquid viscosity is neglected. In the absence of surface tension a finite time singularity whose properties are analysed is formed and the liquid touches the solid on a circle. When surface tension is taken into account, a thin jet emerges from the zone of impact, skating above a thin gas layer. The thickness of the air film underneath this jet is always smaller than the mean free path in the gas suggesting that the liquid film eventually wets the surface. We finally suggest an aerodynamical instability mechanism for the splash.

• Curvature singularity and film-skating during drop impact (PDF)
  L. Duchemin & C. Josserand, 2011, Phys. Fluids, vol. 23, 091701 (2011).
• Rarefied gas correction for the bubble entrapment singularity in drop impacts (PDF)
  L. Duchemin & C. Josserand, 2012, C. R. Mecanique, vol. 340, 797–803.

Liquid ligaments (With L. Vincent, S. Le Dizès and E. Villermaux)

We study the breakup of an axisymmetric low viscosity liquid volume (ethanol and water), held by surface tension on supporting rods, when subject to a vigorous axial stretching. One of the rods is promptly set into a fast axial motion, either with constant acceleration, or constant velocity, and we aim at describing the remnant mass \( m \) adhering to it. A thin ligament is withdrawn from the initial liquid volume, which eventually breaks-up at time \(t_b\). We find that the breakup time and entrained mass are related by \(t_b \sim \sqrt{m/\sigma}\), where \(\sigma\) is the liquid surface tension. For a constant acceleration \(\gamma\), and although the overall process is driven by surface tension, \(t_b\) is found to be independent of \( \sigma\), while \(m\) is inversely proportional to \(\gamma\). We measure and derive the corresponding scaling laws in the case of constant velocity too.

• Remnants from fast liquid withdrawal (PDF)
  L. Vincent, L. Duchemin & E. Villermaux, 2014, Phys. Fluids, vol. 26, 031701.
• Forced dynamics of a short viscous liquid bridge (PDF)
  L. Vincent, L. Duchemin & S. Le Dizès, 2014, J. Fluid Mech., vol. 761, 220–240.