Julien Chopin

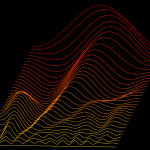
We investigate the wrinkling dynamics of an elastic filament immersed in a viscous fluid submitted to compression at a finite rate with experiments and by combining geometric nonlinearities, elasticity, and slender body theory. The drag induces a dynamic lateral reinforcement of the filament leading to growth of wrinkles that coarsen over time. We discover a new dynamical regime characterized by a timescale with a non-trivial dependence on the loading rate, where the growth of the instability is super-exponential and the wavenumber is an increasing function of the loading rate. We find that this timescale can be interpreted as the characteristic time over which the filament transitions from the extensible to the inextensible regime. In contrast with our analysis with moving boundary conditions,
Biot’s analysis in the limit of infinitely fast loading leads to rate independent exponential growth and wavelength.

Reference :
Dynamic Wrinkling and Strengthening of a Filament in a Viscous Fluid, J. Chopin, M. Dasgupta and A. Kudrolli, Phys. Rev. Lett. 119, 088001 (2017)

We address the mechanics of an elastic ribbon subjected to twist and tensile load. Motivated by the classical work of Green and a recent experiment that discovered a plethora of morphological instabilities, we introduce a comprehensive theoretical framework through which we construct a 4D phase diagram of this basic system, spanned by the exerted twist and tension, as well as the thickness and length of the ribbon. Different types of instabilities appear in various corners of this 4D parameter space, and are addressed through distinct types of asymptotic methods. Our theory employs three instruments, whose concerted implementation is necessary to provide an exhaustive study of the various parameter regimes: (i) a covariant form of the Foppl-von Karman (cFvK) equations to the helicoidal state necessary to account for the large deflection of the highly-symmetric helicoidal shape from planarity, and the buckling instability of the ribbon in the transverse direction; (ii) a far from threshold (FT) analysis which describes a state in which a longitudinally-wrinkled zone expands throughout the ribbon and allows it to retain a helicoidal shape with negligible compression; (iii) finally, we introduce an asymptotic isometry equation that characterizes the energetic competition between various types of states through which a twisted ribbon becomes strainless in the singular limit of zero thickness and no tension.

Reference :
Roadmap to the morphological instabilities of a stretched twisted ribbon, J. Chopin, V. Démery and B. Davidovitch, J. Elasticity, 119, 137-189 (2015)

We investigate the nucleation, growth, and spatial organization of topological defects with a ribbon shaped elastic sheet which is stretched and twisted. Singularities are found to spontaneously arrange in a triangular lattice in the form of vertices connected by stretched ridges that result in a self-rigidified structure. The vertices are shown to be negative disclinations or e-cones which occur in sheets with negative Gaussian curvature, in contrast with d-cones in sheets with zero-Gaussian curvature. We find the growth of the wrinkled width of the ribbon to be consistent with a far-from-threshold approach assuming a compression-free base state. The system is found to show a transition from a regime where the wavelength is given by the ribbon geometry, to where it is given by its elasticity as a function of the ratio of the applied tension to the elastic modulus and cross-sectional area of the ribbon.

Disclinations, e-cones, and their interactions in extensible sheets ,
J. Chopin and A. Kudrolli, Soft Matter 12, 4457 (2016)